Big-O 표기법
업데이트:
Big-O 표기법이란?
빅오 표기법은 알고리즘의 성능을 수학적으로 표시해 주는 표기법입니다.
알고리즘의 시간 효율성을 의미하는 시간 복잡도와 메모리 효율성을 의미하는 공간 복잡도를 나타낼 수 있습니다.
알고리즘의 실제 러닝타임을 표시하는 목적이 아닌, 데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는 것이 목표이기 때문에 상수와 같은 숫자들은 1이 됩니다.
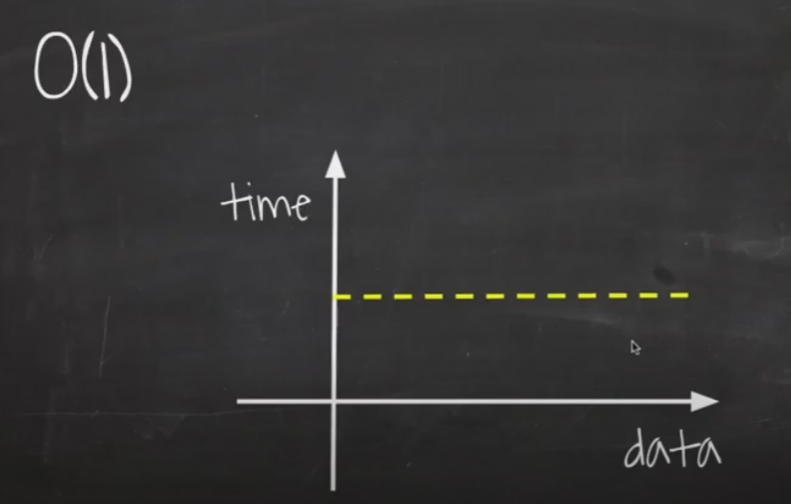
O(1)
입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘을 말합니다.
public void f(int[] n){
System.out.print( n[0] == 0? true : false);
}
인자로 받는 배열의 크기와는 상관없이 언제나 배열의 첫 번째 인덱스의 값만을 확인합니다.
언제나 일정한 속도로 결과를 반환하게 됩니다.
이러한 알고리즘을 O(1)의 시간 복잡도를 가진다고 합니다.
데이터가 증가해도 처리 시간에 변화가 없습니다.
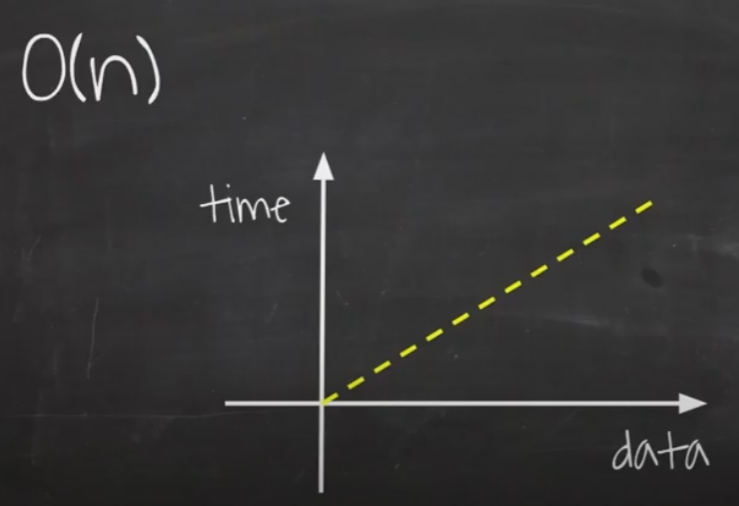
O(n)
입력 데이터의 크기에 비례해서 처리시간이 걸리는 알고리즘을 표현할 때 사용합니다.
public void f(int[] n){
for(int i=0; i<n.length;i++) {
System.out.print(i);
}
}
n 개의 데이터를 받으면 n 번 반복문이 진행됩니다.
데이터가 증가할 때마다 반복 횟수가 증가되어 n의 크기만큼 처리 시간이 증가되게 됩니다.
데이터가 증가함에 따라 처리시간도 같이 증가합니다.
언제나 데이터와 시간이 같은 비율로 증가하기 때문에 그래프가 직선으로 표현됩니다.
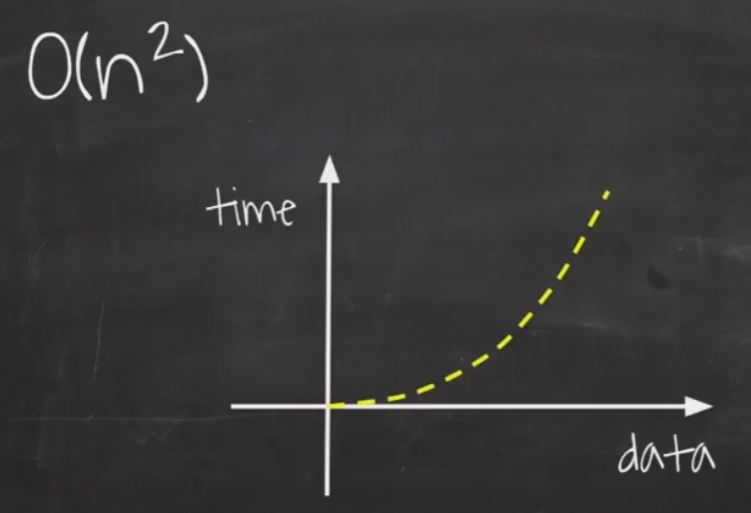
O(n²)
n으로 반복되는 반복문 안에서 n을 이용해 다시 한번 반복문을 실행해 n²가 됩니다.
public void f(int[] n){
for(int i=0; i<n.length;i++) {
for(int j=0; j<n.length;j++) {
System.out.print(i+j);
}
}
}
n개의 데이터를 받으면 첫 번째 루프에서 n번 반복하며 각각의 요소에 접근해 n번씩 반복문을 또 돌게 됩니다.
n을 가로 세로 길이로 가지는 면적만큼 반복이 진행됩니다.
데이터가 커질수록 처리시간이 증가하게 됩니다.
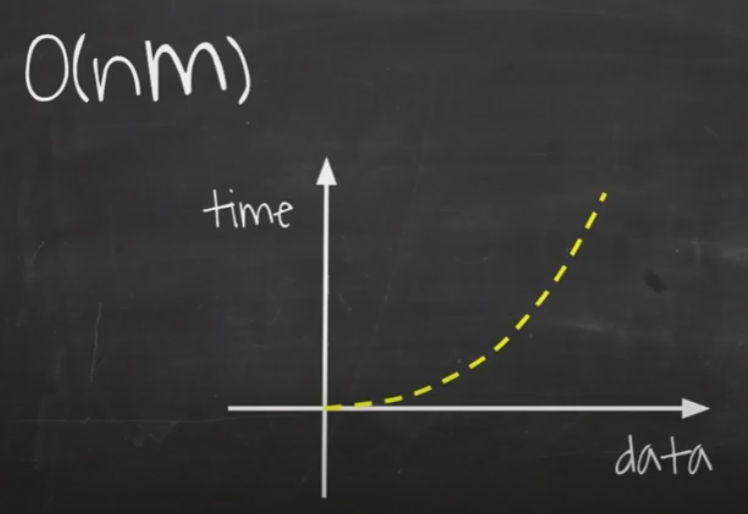
O(nm)
n을 이용한 반복문안에서 m을 n만큼 반복하는 반복문을 실행합니다.
public void f(int[] n, int[] m){
for(int i=0; i<n.length;i++) {
for(int j=0; j<m.length;j++) {
System.out.print(i+j);
}
}
}
n은 크고 m은 작을 가능성도 있기 때문에 변수가 다르다면 Big-O 표시법에도 다르게 표시해 줘야 합니다.
O(n²)과 마찬가지로 데이터가 증가함에 따라 그래프가 수직에 가까워집니다.
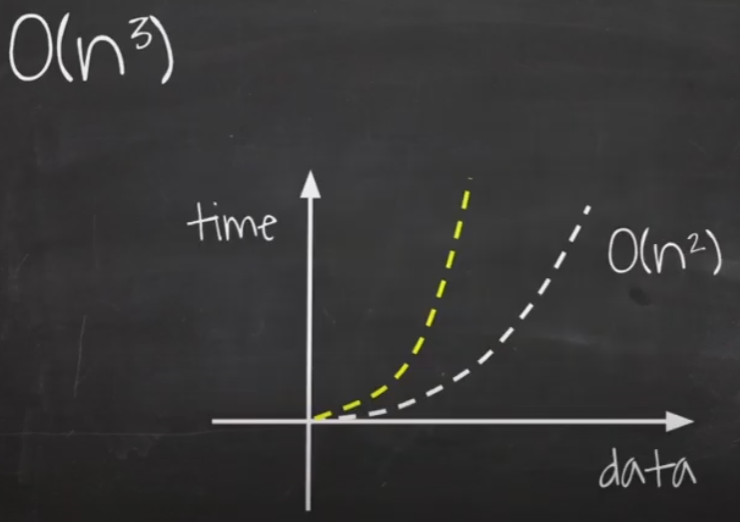
O(n³)
n으로 반복되는 반복문 안에서 n을 이용해 다시 한번 반복문을 실행하고, 그 안에서 다시 n번 반복해서 n³가 됩니다.
public void f(int[] n){
for(int i=0; i<n.length;i++) {
for(int j=0; j<n.length;j++) {
for(int k=0; k<n.length;k++) {
System.out.print(i+j+k);
}
}
}
}
n²을 n만큼 더 반복해서 큐브 모양이 됩니다.
O(n²)과 비슷한 양상을 보이지만, 데이터가 늘어날 때마다 가로, 세로의 높이까지 더해져서 데이터가 증가함에 따라 처리 시간이 더 많이 증가되게 됩니다.
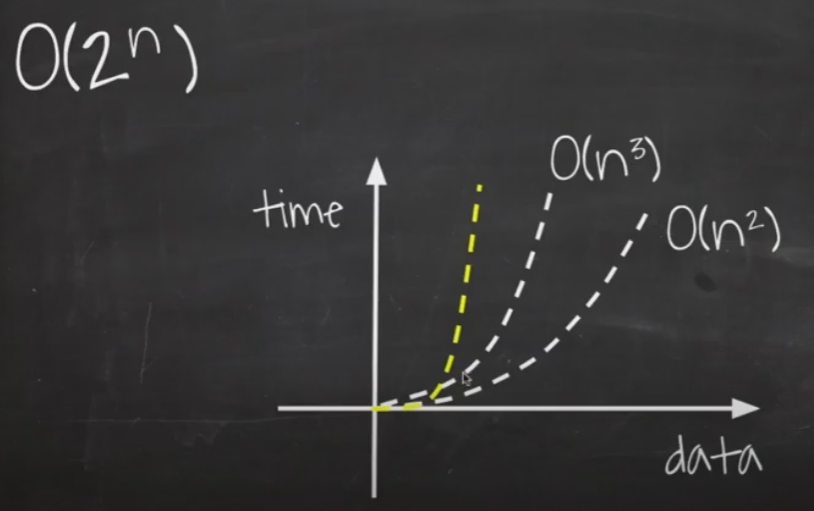
O(2ⁿ)
O(2ⁿ)는 피보나치수열과 비슷합니다.
피보나치수열은 1부터 시작해서 한 면을 시작으로 정사각형을 만듭니다.
1,1,2,3,5,8 = n번째 데이터는 n-1 , n-2 값의 합입니다.

자료출처
public int F(int n) {
if(n<=1) {
return n;
}else {
return F(n-2) + F(n-1);
}
}
매번 함수가 호출될 때마다 두 번씩 호출이 되고, 트리의 높이만큼 반복하는 것입니다.
재귀함수 : 호출한 함수가 자기 자신을 호출하는 행위
데이터가 증가함에 따라 처리 시간이 현저하게 증가됩니다.
O(mⁿ)
m개씩 n번 늘어나는 알고리즘을 표현하는 방법입니다.
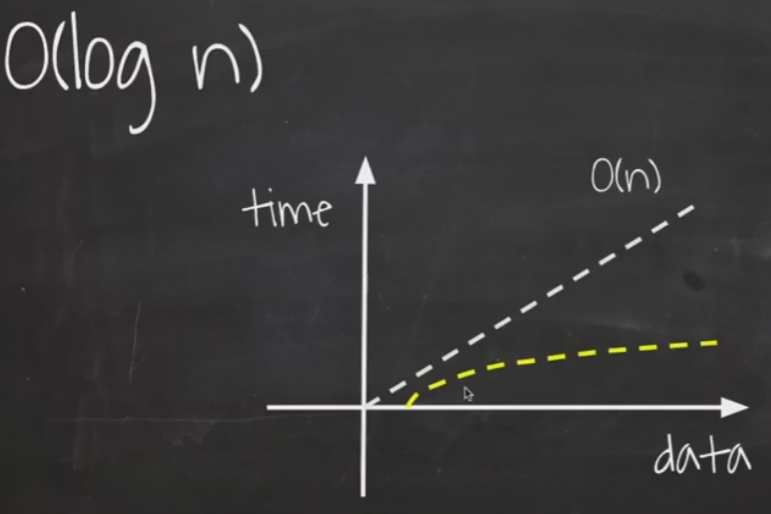
O(log n)
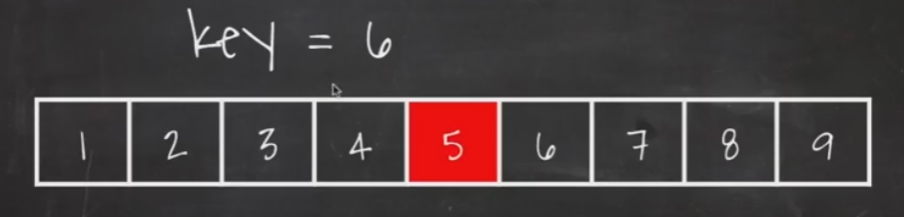
log n의 대표 알고리즘은 이진검색입니다.
이진검색 : 검색 범위를 줄여 나가면서 원하는 데이터를 검색하는 알고리즘
원하는 값을 찾기 위해 우선 가운데 값을 찾아서 key값과 비교합니다.
key값이 가운데 값보다 더 크다 : 오른쪽에 있다는 의미
앞쪽에 있는 데이터들을 확인할 필요가 없습니다.
뒤쪽 데이터들 중 중간값을 찾아서 key값과 비교합니다.
key 값이 가운데 값보다 작다 : 앞 쪽에 있다는 의미
뒤쪽에 있는 데이터들을 확인할 필요가 없습니다.
필요 없는 데이터를 제외하니 key값을 찾았습니다.
처리가 진행될 때마다 검색해야 되는 데이터의 양이 절반씩 줄어드는 알고리즘을 O(log n) 알고리즘이라고 합니다.
public int F(int[] arr, int a, int b, int c) {
// a= 찾으려는 값 , b=탐색 범위의 첫 인덱스, c=탐색 범위의 마지막 인덱스, mid=탐색 범위의 중앙값 인덱스
if(b>c) return -1;
int mid = (b+c) / 2;
if(arr[mid] == a) {
return mid;
}
else if(arr[mid]>a) {
return F(arr,a,b,mid-1);
}
else {
return F(arr,a,mid+1,c);
}
}
처음 호출될 때, 시작 번호인 b는 0, c는 배열의 맨 마지막 번호를 가지고 있습니다.
데이터가 증가해도 처리 시간이 크게 차이 나지 않습니다.
O(sqrt(n))
square root 란?
√100 = 10 -> 100 = 10 X 10
√9 = 3 -> 9 = 3 X 3
n = 9 -> n을 정사각형에 채우면 맨 위의 한 줄이 제곱근 입니다.
정사각형에 n을 채운 후, 맨 위 한 줄만 돌리는 알고리즘이 O(sqrt(n))입니다.
Big-O에서 상수
Big-O 표기법에서 상수는 버립니다.
public void f(int[] n) {
for(int i=0; i<n.length;i++) {
System.out.print(i);
}
for(int i=0; i<n.length;i++) {
System.out.print(i);
}
}
이 코드의 시간 복잡도는?
n만큼 두 번 반복되기 때문에 O(2n) 만큼의 시간이 걸립니다.
그러나 Big-O 표기법에서는 O(2n)을 O(n)으로 표시합니다.
왜? Big-O 표기법은 실제 알고리즘의 러닝 타임을 계산하는 것이 아니라 장기적으로 데이터가 증가함에 따른 처리 시간의 증가율을 예측하기 위해 사용하는 표기법이기 때문입니다.
상수는 고정된 숫자이기 때문에 증가율에 영향을 미칠 때 언제나 고정된 상수 만큼씩 영향을 미칩니다.
증가하지 않는 숫자(상수)는 신경 쓰지 않습니다.
공유하기
Twitter Google+ LinkedIn

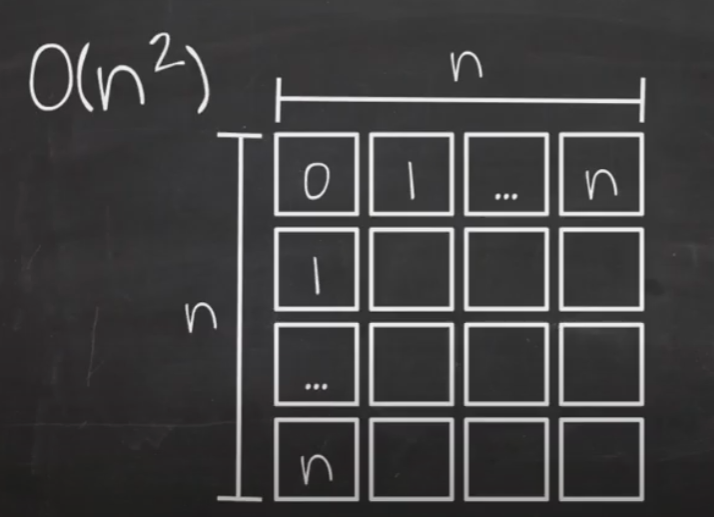
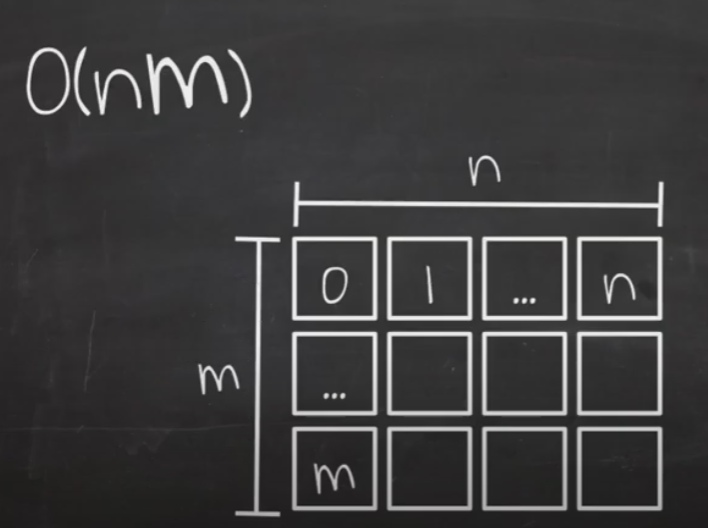

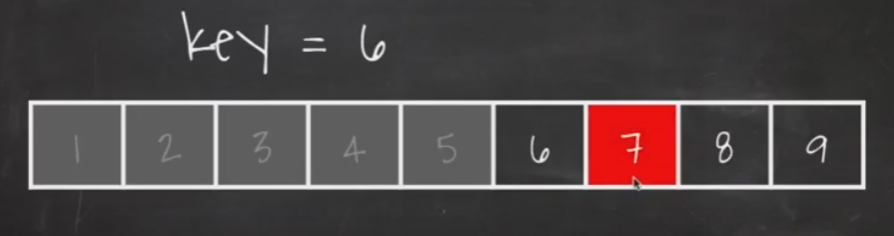
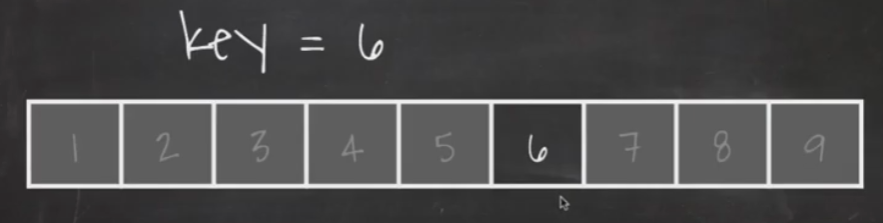
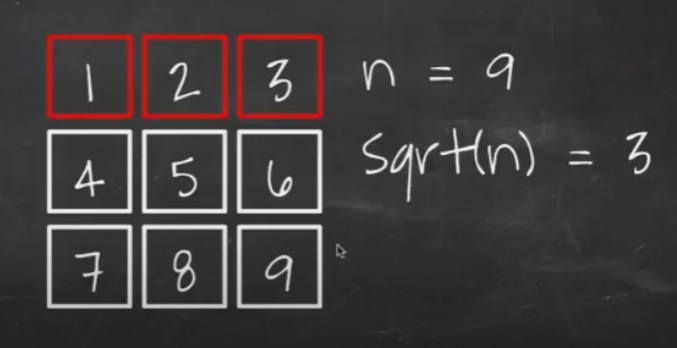
댓글남기기